Steam Calculator - Superheated Steam

This page contains a steam table calculator and information on reaction rates, reaction equilibrium constants and chemical process productivity analysis.

The steam calculator will give you the type of phase (gas and/or liquid) at a given temperature and pressure.

The steam calculator will be able to provide saturated conditions and saturated properties (at Psat and Tsat) for a chosen pressure.

The base for the enthalpy in the table below is incompressible water at 0°C.

 

For other units click here.  For determining the kg/hr. for a steam generator please click here.

Calculation Units

How to enhance the industrial production efficiency of a chemical or ionic process?

 

Short Answer: Increase the temperature of the process gas or steam.  Why? Because this is one easy method today to increase productivity and energy efficiency?  Why save energy?

More Detailed Answer:  Please read on....for high temperature steam and the novel open-ionic products.

 

To enable an increase in the productivity of a chemical or materials processing method, the ojective is to increase the conversion rate of reactants to products.  The term industrial-productivity, encompasses not only the chemical kinetic rate but also aspects of the long-term product life-cycle and other important economic factors that define the reactant and other supply processes (see also innovation constants).   Below, we focus mainly on the the technical variables that influence this productivity (sometimes also referred to as activity in the productivity literature). 

 

As a rule of thumb, an increase in the productivity of an heat-enabled favorable reaction, measured in throughput increase per unit time (e.g. tons per year) may be enhanced by tweaking the process variables like temperature, the pressure or enhancing heat transfer rates where applicable.  The four bullets below show that the productivity can be mainly enhanced by an increase in the Temperature (T), only somewhat by Pressure (P) and sometimes with the use of a good Catalyst.  The direction of any reaction is influenced by the Equilibrium Constant, K (defined below). K is is a thermodynamic property thus implying some strict boundaries for the possibilities to influence this number without changing other variables like temperature.   For chemical reactions the productivity can be considerably influenced by changes in the imposed process conditions.  The rate of reaction involves the equilibrium constant and a few other kinetic 'processing variable' discussed below. Process variables are initial temperature, pressure, concentration of reactants and other pertinent conditions like the quality of insulation, feed back control-ability, good sensors and like.  Overall the productivity of a Commercial Chemical Process is defined as the amount of product made by an industrial chemical reaction plant (units of tons/year).   Improvements in productivity are achieved through improved operation-research optimization methods, good internal business practices and best technical conditions that keep up with the latest technical improvements in thermal and materials availability.  Better productivity generally leads to better energy efficiency. Productivity and production-amount activity are interchangeable terminologies. The symbols R and E below represent the Universal Gas Constant and a generic activation barrier respectively.  R=8.314 J/mol.K (0.0831 bar dm³ mol^-1 K^-1).  The commonly employed unit for E, is kJ/mol for chemical reactions. 

 

The main factors that influence productivity are shown in the highlighted table below.  Productivity is increased by:

• Increasing the Temperature. The Temperature impacts the Reaction Rate, Energy Efficiency, Heat-Transfer Rate and the Equilibrium Constant. The temperature (T) speeds up a conversion exponentially, because the productivity is proportional to (T^ø. e^-E/RT). The power law exponent ø, is a constant approximately equal to 1 but could be as high as 4 for high-temperature processing, particularly when transferring heat quickly with e-ions or very high temperature steam. The Cascade e-Ion plasma is one of the fastest methods of enhancing power in the heat transfer mode.  The ions augment convective and radiative heat transport.  Temperature has an influence on the rate of heat transfer, regardless of whether the reactants are solids, liquids or gasses.
• Increasing the Pressure. The Pressure only somewhat increases the Reaction Rate, only influencing the rate in a manner similar to a reactant concentration-change.  Pressure has a very small or no influence on the Equilibrium Constant,  discussed further below. The impact of pressure is related to achieving more reactant (molecular level) collisions per unit time, which is a possibility when gasses are involved in the reaction.  There is almost no impact of pressure when no gasses are involved in the reaction unless one is in the very high 10-1000 Bar range of operational pressures.
• Increasing the throughput with improved time-management processes.  For example one prefers continuous processing over batch processing or choose open system processing over closed system processing.  A temperature increase, should it be feasible, still has the most dominant influence on production.  However such an impact is dependent on how many years that the company has been in existence!...i.e.  where the company is in it's long-term cycle life (long-term product life-cycle).   Note when conducted at the appropriate part of the long-term life cycle, a planned temperature increase is relatively easier and cheaper to implement when compared to certifying and creating high pressure containment methods.  One may select and scale the feed rate for continuous reactors a bit more easily than for batch reactors -  again provided it is at the proper time in the life cycle.
• Improving the temperature uniformity and optimizing the type of energy transfer mechanism for the desired uniformity.  Typical energy transfer mechanisms of interest are normally convection, radiative, with a e-Ion types of energy transfer/efficiency enhancer.  Use hybrid thermal processes for best outcome for energy efficiency and productivity.  Using preheated reactants is a productivity enhancer. The OAB technology is a modern technology for high temperature steam.  Gasses can be easily heated with the efficient Airtorch process-heater technology.  Solids and liquids may be preheated with MagnaCoils, Robust Radiators, high temperature hot plates or with safe energy-efficient furnaces.

 

Reaction rates increase when the possibility of making reactant molecules encounter each other quickly is enhanced.  As discussed pictorially below, in the reaction rate section, such an increase can be enabled in several ways. Both exothermic and endothermic reactions rates are increased when the temperature of the reaction is increased. Reaction rates increase exponentially with Temperature. The best available catalysts should always be used as they impact activation energy.  Open processes i.e. steady state flow is a continuous process, are almost always more energy efficient than a batch process – e.g. high pressure steam batch-sterilization is slower than continuous high temperature steam sterilization if it is allowed (note: the steam must be of a correct and approved quality). The use of high pressures for open processes is very difficult and expensive.  Today, with the advent of new transformative thermal devices, like the e-ion and the OAB, the temperature of processing can be easily increased even for for open-flow processes.  Significant advantages can be gleaned for energy efficiency.

 

 

Equilibrium Constant of a Reaction.

 

Assume a hypothetical reaction: aA + bB +mM--> yY + zZ+mM.  Here Z and Y are the product species.  A and B are the reactant species.  M is a species inert to the reaction.  A chemical reaction conserves mass and the total number of atoms of all elements involved in the reaction.  If all species are gaseous we write the reaction with the (g) in parentheses to indicate gaseous species e.g. aA(g) + bB(g)+mM(g)--> yY(g) + zZ(g)+mM(g). The lower case letters x, y, a, b, m are moles. The arrow signals the direction of reaction that is of interest. 

 

This same reaction in its stoichiometric form may be written as a₀A(g) + b₀B(g)+ m₀M ⇔ y₀Y(g) + z₀Z(g)+ m₀M, the two way arrow indicates that a forward and backward reaction are feasible. The stoichiometric form is not necessarily the equilibrium mixture. 

 

When at equilibrium i.e. a_0e, b_0e, y_0e, z_0eare present of each species respectively.  Let us designate the equilibrium mix in its most general form as a_0eA(g) + b_0eB(g) ⇔ y_0eY(g) + z_0eZ(g).  Regardless of how we represent the reaction, the chemical reaction conserves the initial mass and the total number of atoms of all elements involved in the reaction.  The equilibrium compositions are not known a priori. Only m₀ is known and the initial amounts of A and B can be known and the stoichiometric form of the equation is known. 

 

The objective of chemical reaction analysis is to find the equilibrium compositions or the direction of the reaction for an initial mix of reactants. From thermodynamics we know that the direction of a reaction is determined by conditions that lower the free energy of an initial mix because of the formation of more thermodynamically stable product mix.  The direction of a chemical reaction is determined by the knowledge that for the equilibrium mix of reactants and products, the reaction will neither go forward or backwards.  In other words, at constant pressure and temperature, the total free energy change between products and reactants of the reaction is zero for the equilibrium mix.  The free energy change is related to the enthalpy and entropy change between products and reactants.  The heat of reaction (enthalpy change), DHr of compounds can be measured or calculated from bond energies or by assigning standard state thermodynamic properties to all elements. The entropies of each element and compounds is also known (see free thermodynamic calculator).  At constant temperature and pressure, the equilibrium mix for a reaction is reached when the total Gibbs free energy change between products and reactants is zero.  Based on this concept, an equilibrium constant, K_ec or Kp (see below for definitions that are based on the relationship with the activity) for every reaction can be defined and is generally known for all reactions by assuming a standard state (see below) i.e. a base level from which all changes are measured.  The equilibrium constant can be calculated from a knowledge of such free energies of the reactants and products at the reaction temperature.   Free energies are measure from a standard state (again see below).  Once known, it can be used to calculate the extent of a reaction that is possible to reach equilibrium conditions and the composition mix at equilibrium.  The equilibrium constant thus is a very useful number because it quickly indicates whether a reaction e.g. the desired forward reaction for example above is possible or not, and how much product may be expected from a chosen reactant mix when the reaction reaches equilibrium or under steady state conditions if the products are continuously removed and reactants are continuously added. The equilibrium constant allows for the determination of y_0e, z_0e in the reaction above, when m₀ is known and the initial amounts of A and B are known.  For the derivations below to illustrate the definition of the equilibrium constant, we will drop the subscripts _oe.  The K_ec (chemistry text books use the symbol Kc) or Kp values are tabulated and well known for almost all chemical and biological reactions. The Equilibrium Constant is the power ratio of activities (e.g. a_Y) (shown below) of products over reactants for a reaction that is at equilibrium.  The equilibrium constant expression is defined as:

K_ec= {a_Y}^y0{a_z}^z0/{a_A}^a0{a_B}^b0

 

The activities can be written in terms of mole fractions, moles/L or partial pressure ratios.  The gaseous reaction equilibrium constant Kp, is expressed by partial pressure ratios.

 

K_P= {P_Y/P0}^y0{Pz/P0}^z0/{P_A/P0}^a0{P_B/P0}^b0

 

Here P0 is a the standard state pressure (normally 25C, 1 atmosphere is chosen for chemical reactions) and P_Y is the partial pressure of gas Y defined as P_Y=(y/ N_T)P_T where P_T is the total pressure including any inert constituents in the gas mixture and total number of moles is N_T including any inert constituents in the gas mixture.  The partial pressure P_z, P_A, P_B are similarly defined.

 

For ideal gasses a_Y= P_Y/P_T.  For pure solid or liquids a_Y~1.  For solutions a_Y=g_Yx_Y.  Where g_Y is called the activity coefficient (ranges from 0 to 1; it is closer to 1 for high concentrations and high temperature), and x_Y is the mole fraction when including all inert species.  Activity coefficients in the standard state are, by definition, equal to 1.

 

When expressed in mole concentrations i.e. mol/L the equilibrium constant is given as K_ec = [C_Y]^y0[C_z]^z0/[C_A]^a0[C_B]^b0  here the square brackets correspond to concentration in moles/L where L is the symbol for liter.  1 dm³= 1 L.  1000 mol/m³= 1 M (molar).   C_Y= (Ny/N_T).Nyo/V where V is the volume of the equilibrium mixture and Nyo is the standard state moles of the species Y (equal to 1). Cy= P_Y.Nyo/Vy0 where Vy0 is the standard state volume and Nyo is the standard state moles.  The density of water is ~ 1000 g/L and its molar mass is 18.02 g/mol (or 1/18.02=0.055 mol/g). Therefore, the molar concentration of for 1 L of water is C_(H2O) = 55.5 mol/L.  Other units may be used.  The concentration may be expressed as mass per liter e.g. for water 1000 g/L or mass per moles e.g. for water 18.02 g/mol.  Below we will use the moles per L definition for molar concentration.  Substituting C_Y= (Ny/N_T).Nyo/V in the Kp equation above yields a Kec number for the equilibrium constant where

 

K_ec = {(C_Y/P0).Vyo/Ny0}^y0{(Cz/P0).Vzo/Nz0}^z0/((C_A/P0).Vao/Na0}^a0{(P_B/P0).Vbo/Nb0}^b0

 

With P0= 1bar and Nyo/Vyo and all other similar species-related quantities equal to 1 Molar (1 mole/L), the equation for the equilibrium constant above takes the familiar form

 

K_ec = [C_Y]^y0[C_z]^z0/[C_A]^a0[C_B]^b0

 

when C is the molar concentration and thus K_ec= {K_p/(P_T) ^∆n0}.  Note that we have defined Cy= P_Y.Nyo/Vy0 and taken P0  =1bar and Nyo/Vyo and all other similar species-related molar volume is equal to 1 Molar (i.e 1 M).

 

K_ecx = {[P_Y/P_T]^y0[P_Z/P_T]^z0}/{[P_A/P_T]^a0[P_B/P_T]^b0}= [Kp{(P0) ^∆n0/(P_T) ^∆n0}]

 

where ∆n0 = (y^_o + z^_o) – (a^_o + b^_o) i.e. (number of moles of gaseous products – number of moles of gaseous reactants for the stoichiometric form of the reaction) i.e. in the balanced chemical reaction. The subscript x in Kecx indicates that the equilibrium concentration is for mole fraction type concentration. 

 

The relation between K_p and K_ecx (same as the symbol Kx, sometimes employed in chemistry textbooks) is given as:  Kp(P0) ^∆n0 = Kecx (P_T) ^∆n0=Kecx (N_TRT/V) ^∆n0  for a volume V (remember the molar volume of an ideal gas is same regardless of the gas and also emphasis the use the correct form of R e.g. if P is in bar then a form of R could be 0.0831 bar dm³ mol^-1 K^-1) (if P is in Pa the R= 8.314J/mol.K).  Note that 1 bar ~100kPa. N_T/V is the molar volume of the ideal gas. Chemical concentrations are the same as molar concentrations in moles/L.   For gases, especially for ideal gasses (that is described by a Equation of State PV=NRT) the Equilibrium Constant Kp is not a function of the total Pressure.  The equilibrium constant will remain the same for each reaction, independent of initial concentrations. The K_ec changes with temperature.

 

For any given temperature, there is only one value for the equilibrium constant. K_ec (or more commonly referred to as Kc when we express the equilibrium constant as a ratio of concentrations) only changes if the temperature of the reaction changes.
If K_ec > 1 then it favors product formation.   In fact if K_ec>1000 then you find mostly products i.e. if you mix A and B, they react almost completely to become product when K_ec>1000.
If K_ec < 1 then it favors the reverse reaction.

 

The dependence of the equilibrium constant with temperature is given by the van't Hoff equation which has a differential form and an integral form i.e. either expressed as d(ln(K_ec)/dT = DHr/RT²  or as ln(K_ec)=-DHr/RT + (a constant of integration).   Increasing the temperature will increase production output because of an increase in Kec (the equilibrium constant) where possible, but more importantly from the significant reaction rate increase that occurs (e.g. enabled with an OAB) when the highest throughput technique and the correct temperature are chosen for the reactant steam.  Regardless, other considerations for a commercial process may often exist which have nothing to do with the reaction kinetics, and a multi-step process may for example be necessitated for a reaction product (see http://en.wikipedia.org/wiki/Equilibrium_constant).  In such cases the use hybrid thermal processing is one techniques get the best outcome. A knowledge of equilibrium constants is essential for the understanding of many chemical systems, as well as biochemical processes such as oxygen transport in blood or other redox reactions in the human body.

Assume again aA + bB -->yY + zZ; with a Heat of Reaction> 0 (endothermic DHr>0).   If net heat is required to inspire this reaction (endothermic), then an increase in temperature causes an increase in the products conversion for the reaction because the K_ec increases.   Almost always we have to enable processes with the addition of heat whether they are chemical, melting, sintering, rolling, forging or ionization processes.  In other words, processes are endothermic for almost all commercial objectives.  Even if exothermic, the processes may present an activation energy barrier (discussed below) which needs to be overcome by a higher reactant temperature before the reaction can go forward.  In order to calculate the amount of Y and Z (products), the equilibrium constant is all that we need once we know the amounts of A and B (the reactants).

Example: Consider the reaction:

C(s) + H₂O(g) ⇔ H₂(g) + CO(g). The thermodynamic equilibrium constant for this reaction is ~ 6.5 x 10^-19 at 298K.  The value of the equilibrium constant (K_ecx) at two higher temperatures is given below for this reaction.   Note that K increases dramatically from less than 1 to above 1 with an increase in the temperature for this endothermic reaction.

Temperature 430C (806F)   K_ecx~= 5 x 10-5
Temperature 700C (1292F)  K_ecx ~= 1.5

For more information on equilibrium constant expressions and tables please visit the Wikipedia site: http://en.wikipedia.org/wiki/Equilibrium_constant. 

Examples where H₂O is a process chemical:

Hydrogen is used in ammonia making, acid making, petrochemicals and as fuel (including fuel cell). The United States alone produces more than 10 million tons of hydrogen per year.  The following examples are for steam reactions are possible for hydrogen manufacture.

3Fe(s) + 4H₂O(g) ⇔ Fe₃O4(s) + 4H₂(g)
From known thermodynamic tables Kc at 500C for this reaction is 5.218E+002 which implies that at this temperature plenty of H₂ is made i.e. the forward reaction is favored. Concentrations of Fe and Fe3O4 are omitted in calculating Kp. Although the concentration of a gas can have various values depending on partial pressure, the concentration of a pure solid or a pure liquid is a constant at a given temperature. The concentration of liquid solvent is usually omitted as well.  For the reaction of iron with steam, you would write  Kp=PH₂⁴/PH₂O⁴ and get the PH₂ value.   The reaction 2Fe + 3H2O(g) = Fe2O3 + 3H2(g) does not go forward above 600C.    The reaction Fe + H₂O(g)= FeO + H₂(g) is very weak by 1000C as is the 3Fe(s) + 4H₂O(g) ⇔ Fe₃O4(s) + 4H₂(g) reaction. In order to make hydrogen with such reactions it is important to find the highest temperature where the reaction remains very favorable as well as show the best kinetics. 

A more commonly employed reaction for making hydrogen is the methane steam reforming reaction (MSR), CH4 + 2H2O ⇔ CO2 + 4H2 for commercial bulk hydrogen production. Steam Reforming can be thought to occur in two steps, namely:
CH₄ + H₂O ⇔CO + 3H₂ [ΔH = +206 kJ mol-1]
CO + H₂O ⇔ CO₂ + H₂ [ΔH = -41 kJ mol-1]
________________________________________________
CH₄ + 2H₂O--> CO₂ + 4H₂ [ΔH = +165 kJ mol-1] Endothermic thus requiring high temperature for both greater and faster conversion.  This reaction can be favorably manipulated with OAB(R) high temperature steam.

 

Steam/Water is employed as a chemical in the photosynthesis reaction to make sugar or sugar-like compounds.   Although written in a simple reaction manner (6CO2 +6H2O > C6H12O6 + 6O2) the reaction is quite a complex reaction.  This reaction, called photosynthesis occurs in plants with the help of sunlight (photons) and uses chlorophyll in the  plant cell chloroplasts. Chloroplasts are small molecular objects that have very specific function in a cell.  Chloroplasts are found in plant cells and some other cellular organisms.  During photosynthesis, chloroplasts capture photons and store the energy of the photons in the energy storage molecules ATP and NADPH all the while releasing oxygen from water. They then use the ATP and NADPH to make organic molecules from carbon dioxide in a cyclic process known as the Calvin cycle.  This cycle requires trapping of sunlight energy during a part of the cycle.  Ongoing e-ion and OAB research is directed at using photons and electrons to possibly simulate and/or aid the sugar synthesis or sequester the CO2.  However the research is at a very early stage. 

 

The E-Ion Cascade is revolutionizing the way nitrogen is used by providing an alternative route to HNO3, which avoids the NH3 intermediate, is direct Nitrogen oxidation to aqueous HNO3 

N2(g) + 2.5O2(g) + H2O(liq) = 2H+(aq) + 2NO3−(aq)

The equilibrium constant for this reaction is ∼2.7 × 10−3 M4/bar3.5 (Standard GibbsFree Energy ΔG₀ = 14.6 kJ/mol N2)

 

Yet another common steam/water reaction is dissolving CO₂ in H₂O and consequently forming a weak acid (bubbly).  This reaction is not the same as the photosynthesis reaction discussed above. The dissolution reaction is used for making soda and soda drinks. There are other similar reactions between elements where more than one compound can be made. The law of multiple proportions then applies.  For the forward reaction to dominate, the equilibrium constant has to exceed 1.  For the MSR reaction, the equilibrium constant increases above 1 only when the temperature exceeds 864K.  At 1000°C Kec=4963 which is very favorable for complete conversion to hydrogen should that be the objective.  New superheated steam generation devices provide instant hot steam to be made available for this and similar reactions.   The reaction C+ 2H2O -->CO2 +2H2 has to be above 966K for the reaction to become feasible for the forward reaction.  MHI also offers air heating for combustible and non-combustible gasses.  Other reported uses uses for high temperature steam are in steam hydrogasification, or in chemical process equipment for heat transfer from superheated steam to a reactor chamber.  For the first time by combining OAB's and Robust MHI furnaces, steam boxes up to 1700C in both the continuous and batch modes are now available.  Reacting Fe with steam is one way of producing H2.

 

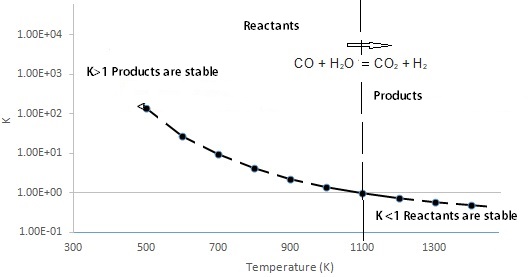
Yet another hydrogen producing reaction, where CO reacts with H2O is an exothermic reaction (see all the way below for schematics of exothermic and endothermic reactions).  Called the Gas Reaction for Hydrogen, this reaction can be used to illustrate how the K changes with temperature for an exothermic reaction where one mole each of CO and H2O (reactants) produce one mole each of CO2 and H2 (products).   Note that the temperature is in Kelvin and the direction of the reaction is as shown.  Note the logarithmic scale of the y-axis for the equilibrium constant.

 

 

 

Ionic Reactions

 

When speaking of ionic reactions, there are two common types:  (a) the aqueous ionic type and (b) the non-aqueous ionic type.  Several standard chemistry textbooks present the aqueous type very comprehensively.  The non-aqueous type is mostly related to ionic gases and ionic gas-solid reactions and the reports are few and far between.  However these are the ones that are industrially very valuable for creating coatings, diamonds, barriers and anti corrosion, and anti seize surfaces.

 

The aqueous type: An ionic equation is a chemical equation where the electrolytes in aqueous solution are written as dissociated ions.  The most important reaction is the dissociation of water i.e. 2H₂O= H₃O⁺ + OH^- where the H₃O⁺ is the hydroxonium ion and OH^- the hydroxide ion.  The square brackets are concentration expressed in moles/liter.  The equilibrium constant for ionic reactions is given the symbol Kw.  For the water dissociation reaction the self-ionization equilibrium constant is Kw=[H₃O⁺][OH^-]=10^-14 at 296.5K.  Water molecules dissociate into equal amounts of H₃O⁺ and OH⁻, so their concentrations are equal to 1.00×10⁻⁷ mol∙dm⁻³ (dm^-3 is a liter) at 296.5K and 0.1MPa.  Note that the water dissociation equilibrium constant is a very small quantity.  A solution in which the H₃O⁺ and OH⁻ concentrations equal each other is considered a neutral solution. When the [H₃O⁺] concentration is high the pH is low (acidic) and for the same equilibrium constant Kw, the the corresponding [OH^-] is low.  The pH of a neutral solution at 294.5K and 0.1Mpa, is pKw/2=7where pKw= -log{[H30⁺][OH^-]}. The self-dissociation ionic reaction is an endothermic reaction.  Following the Van't Hoff rule discussed above, the self dissociation increases with increasing temperature.  Therefore the pH number decreases with temperature as does the neutral point.  When there is an abundance of H₃O⁺ formation (for the same Kw) then the solution is considered a very strong acid.  Although a pH of close to zero reflects an extremely strong acid, the pH scale is not a very useful scale for extremely strong acids such as 2M HCl.  When water is made into gas (steam), then dissociating the gas into atoms or further into ions, is very difficult (see table below) unless the LIP or other means is used for ionization.  The temperature thus decreases the pH (note pH is the -log of the H⁺ concentration written as pH= -log[H⁺], or more correctly the -log of the H30⁺ concentration).  Pressure decreases the Kw number for the water self-dissociation reaction. A thousand-fold increase in pressure will reduce Kw to about 10^-13.  The value of K_w is usually of interest for the liquid phase dissociation. Example values for superheated steam (gas) including for supercritical fluid are given in the reference http://en.wikipedia.org/wiki/Self-ionization_of_water.

 

Other examples of aqueous ionic reactions are e.g. Ag⁺(aq) + NO₃^-(aq) + Na⁺(aq) + Cl^-(aq) → AgCl(s) + Na⁺(aq) + NO₃^-(aq), an ionic equation of the chemical reaction: AgNO3(aq) + NaCl(aq) → AgCl(s) + NaNO₃(aq).

The non-aqueous type of ionic reactions: With the advent of the  Cascade e-ion technology, easy ionization is now offered by energy efficient steady-flow devices.   A positive ion is a chemical species (chemical atom minus electron) i.e. an element separated from at least one of its electron.  A negative ion has at least one extra electron compared to the neutral species.  Using easily made cascade e-ions has opened a new window to an undiscovered realm of chemical and metallurgical reactions with extremely high production rates.  More details are available by clicking on new transformative commercial ion and electron making devices.   With the the e-ion rapid kinetics can be invoked to give clean shiny aluminum, copper and other metallic finishes.  Ammonia can be made.  E-Ion machines save energy as they use only air to create biomedical and hard tool bit surfaces.  In fact, one of the biggest breakthroughs for aluminum dross reduction comes from using a thermally ionized air-cover over a melt.   Ionic deburring, peening and such reactions are being discovered for anti-seize and anti-corrosion use with the Cascade e-Ion. The e-ion technology has also lowered the cost of cleaning VOC containing gasses per pound of gas cleaned.  Ionic reactions can be used to create diamond films or other hard films on substrates by using the right precursors.   A single 15kW unit of an e-ion reduces dross in aluminum, bismuth, zinc, lead, silver and other materials.  Surface charge and wettability of plastics can be changed in a fraction of a second.  Such changes influence the antimicrobial character of the surface.  Ionization is often reported in eV/atom and chemical reactions in kJ/mol.  The conversion is:

 

1 eV/atom = 23.069 kcal/mol = 96.521 kJ/mol 

 

Typical ion and boson or fermion reactions with molecules are classified typically into the six groups listed below.  A^ indicates activated species.

 

e− +A2 −→ 2 A^ + e−

e− +A2 −→ A^2 + e−

e− +A2 −→ A+ +A− + e−

e− +A2 −→ A+2 + 2e−

e− +A2 −→ A− +A^

e− +A2 −→ A+ + A + 2 e−

 

With ionic reactions where air can be ionized, the most important breaktrough may be that simple high speed tool drills and tool bits and tapping drills can be made to have a very hard, smooth and ant-galling coating with extremely good coefficient of friction thus cutting machining speeds some times by half.  More about boson and fermion devices.

 

Hydrogen peroxide often figures in many ionic reactions. This compound uniquely is able to act as an oxidizing agent or a reducing agent.  When it acts as a reducing agent, oxygen gas is produced.  It can also act as an oxidizing agent for example for the oxidation of ferrous oxide Fe2+ to the Fe3+ oxidation state.  Ionized H₂O is now offered by a special e-ion machine.  Ionized H₂O appears to be particularly useful for creating antibacterial plastic surfaces although the tests to date are only of a limited nature.

 

The benefits are being discovered on a daily basis.  Cascade e-Ions easily ionize Helium, Argon, forming gas (Ar+H₂), and most importantly air to forming a reducing plasma plume.  In time physicists and chemists will discover the exact nature of the Cascade e-Ion plasma and determine whether the Saha-Langmuir equations are valid and how the Townsend avalanches, impact the Cascade e-ion plume.   Much is to be learnt.  The company MHI Inc.  which has invented these plasma systems has also made them available at a fraction of the price compared to other industrial plasma systems.

 

How to make a rusted part, better protect itself from corrosion, after it shows corrosion (i.e. looks red and rusted)?  Try to clean it and apply a non corrosive paint.  If the application is more demanding and may need to be used at a higher temperature then one way is to employ the SE mode of the Cascade e-Ion to easily treat the rusted part.  Although microstructure details are not yet fully understood it does appear that ensuring that Fe₃O₄(s) are ionically fused-in compared to Fe₂O₃(s) along with certain compound nitride phases.  Such surfaces are enabled by the Cascade e-ion in the SE mode above a certain temperature as discussed above for steam.  The Cascade e-ion further allows oxynitrides to form which impart significant smoothness and less seizing.

 

Reaction Rates for Exothermic and Endothermic Processes.

 

Variables that increase the rate of a reaction i.e. the technical productivity include the specific species of the reaction, the specific activated species that form during the reaction, the reactant concentrations, surface area, temperature, life-cycle placement and catalysts.

 

 

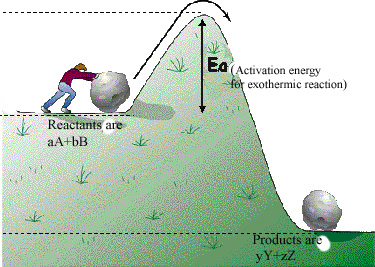
For a reaction to occur at a certain temperature, an initial activation energy barrier may required to be overcome.  Reactants have to collide to produce products and because this is a rate limiting step, chemical reactions encounter a barrier.   Please refer to the figures below for a pictorial description and an analogy.  The Activation Energy Barrier, E_a is the minimum energy that a reactant mix must possess in order to convert the reactants to products.  This activation barrier (Ea) can determine how fast a reaction occurs.   The higher the activation barrier, the slower the reaction rate.  The lower the activation barrier, the faster the reaction.  Consider the analogous process of someone trying to roll a boulder over a hill.  The higher the hill,  the slower the task.  The lower the hill, the faster the process.  The height of the hill is analogous to the energy of activation (Ea) that has to be overcome for a reaction.

 

Assume again a hypothetical reaction: aA(g) + bB(g) ⇔ yY(g) + zZ(g).  Assume we are only interested in the forward reaction i.e. aA(g) + bB(g) --> yY(g) + zZ(g) i.e. we are interested in the production of Z and Yas the objective.  Assume we are further interested in producing Z and Y as quickly as possible in order to have the highest productivity (production rate). The applicable rate equation is now discussed (link to example for oxides).

 

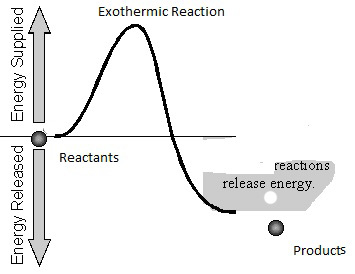
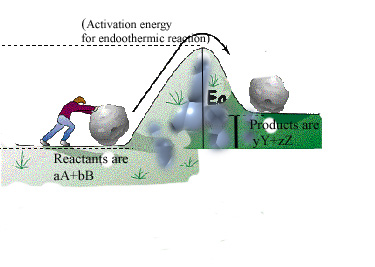
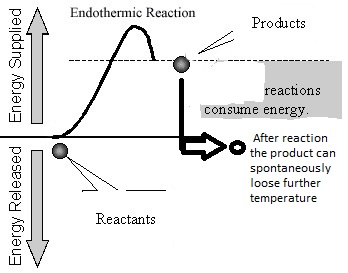
Regardless of being exothermic or endothermic there is an initial barrier Ea, to overcome for the forward reaction.  Increasing the temperature of the reaction is the same as providing higher energy (temperature) reactants. The difference between an exothermic and endothermic reaction can be illustrated by the hill/boulder analogy illustrated below.  After reaching the top of the hill if the boulder rolls to a height lower than the original, it will possess a lower potential energy than at the start.  The difference in energy is the net gain of energy from the process - note the analogy with an exothermic reaction e.g. H2+1/2O2= H2O in the diagrams below where there is a heat release because some bonds are broken and others made or remade.  If on the other hand the boulder comes to a rest at a higher level than the start, the difference in energy is the amount supplied during the process.  The endothermic reaction analogy where a part of this supply of heat energy is captured in the new chemical bonds e.g. CH4 + 2H2O --> CO2 + 4H2 and higher temperature, illustrated by the thick vertical line in the right hand side figure below.  Regardless, for both examples, Ea is the amount of energy to be overcome and needs to be initially made available to the reactants.  For both examples, the free energy change (work required to carry out a reaction) has to be favorable (strictly at least for one sub-reaction if there are several sub reactions in the overall reaction).  When the net free energy change is negative (the reaction can produce work) the reaction can be spontaneous, yet may still need to overcome an activation energy barrier.  When the free energy change is positive there is a net energy penalty which may be lower than the activation barrier.

 

Although the overall production expression is of the form given all the way at the top of this page, note that a major part of the rate could be from the commonly understood reaction rate equation.  The symbol most often employed for the rate constant is lower case k. The reaction rate equation for a chemical reaction is  proportional to e^-Ea/RT.   The rate of reaction, in either reaction direction, is related to the initial concentration raised to a power that reflects the order of reaction, multiplied by a pre-exponential constant k₀ and further multiplied by e^-Ea/RT.   Ea may not be strongly influenced by temperature, but k is exponentially increased (very strongly influenced) by an increase in the temperature.  The e^-Ea/RT part of the rate constant does not have dimensions but the amount made per unit time e.g. Kg/hr, is proportional to the initial starting amount and to k₀; and thus scales with the temperature.   Catalysts are used to essentially reduce the effective activation barrier (Ea) for any reaction by providing a new reaction pathway that has a lower or smaller barrier (note that an apparoximate analogy with the boulder example could be making the hill surface smoother).  However, catalysts may foul over time and are often very expensive (many catalysts contain expensive noble metals like platinum).  Increasing the temperature is thus often the best bet on a cost basis to enjoy higher productivity.

 

The commonly used units for Ea are kJ/mole or less commonly used are kJ/(volume units). R is the universal gas constant.   Ea is a barrier that needs to be overcome and RT is a thermal "help' energy term.  The ratio Ea/RT is dimensionless.  Note that T is the temperature in Kelvin.  Ea is a term which has the order of energy requirement of chemical bond energies.  Chemical bonds have bond energies in the order of 10-100kJ per mole whereas R is 8.314J/mol.K.  The value of RT only above T >1000K brings the RT term into the order of magnitude of common chemical bond energies.  The pre-exponential part, k₀ (with units of frequency i.e. 1/s) is also a function of temperature.  It increases with temperature in a close-to-linear relationship according to a theory called the activated species theory.  Note that Ea may simply be the real endothermic energy requirement for a reaction, if an activated complex is not relevant to the reaction sequence.  However almost always a activation energy component exceeding the total thermodynamic-barrier requirement is required to start and keep a reaction ongoing.  Ionic reactions are particularly interesting in this regard and will be discussed in a later chapter of this module.  For completion we should also note that oscillatory reactions can be set-off because of kinetic rate differences in sub-reactions.  Some of these types of reactions are called BZ reactions.  Such oscillations when present offer an ability to alter the type of the final product based on the initial temperature choice made.

 

Again one may be able to sense an analogy from the common experience of trying to push a boulder over a hill.  The high and low barrier definitions are relative (think of the analogy of height and surface of the hill vs. the might and will of the person pushing the boulder).   For the same hill height, a lower surface resistance (friction) and greater will power makes it easier to push the boulder up the hill.  In a similar manner the activation energy however large is overcome when the reactants are properly energized which is easy to do with temperature.  Because e^-Ea/RT = 1/e^Ea/RT, note that this exponential term is almost zero when the exponent is large i.e. (Ea>>RT).  The exponential term is almost maxed out at one when (Ea<<RT).    Although the temperature is thus noted to strongly impact the "will and might" of the reactants in an exponential manner, the influence on the overall kinetics comes also from the rate of heat transfer which increases directly with T⁴ for radiation and even more with plasmization enhanced heat transfer (see also all the way above on this page for overall rate equation).  An increase of the pre-exponent terms in the reaction rate equation further speeds up the process.  Further enhancements to production speed can come from life-cycle placement issues and the associated innovation constants.  Therefore increasing the reaction temperature (or reactant temperature) dramatically increases productivity.  Thus the temperature plays a very dominant role in the determination of productivity.  For more references - choose any search engine like Google, Yahoo or Bing or any other and type in the key phrase " How is productivity influenced by high temperature, including high temperature capable MHI heating materials". 

 

 

 

 

 

 

 

 

How does one ensure that the forward reaction is the only one occurring? Will equilibrium conditions prevail and equalize the forward and backward reaction rates?

 

All reactions tend towards equilibrium.  When Kec (or any of the other K's like Kp or Kw) is greater than about 1000, the reaction is slam dunk forward moving.  If less than about 0.001 the reaction is almost slam dunk completely reverse.   For such reactions the equilibrium constant is clearly understood as impacting the rate of reaction in a particular direction.  For reactions that are not lop-sided (i.e. K between 0.0001 and 1000), there will be a mixture of reactants and products at equilibrium when starting from a non-equilibrium reactant mix.  The paragraph below discusses methods to optimize the yield for such cases.

 

For increased productivity the objective is to quickly consume the reactants to make product.  One common method is to maintain the system far from equilibrium with more reactants present than what should be present at equilibrium.  The objective is to find physical techniques like isolating and cooling the products in order to reduce the back reaction rate.  For the hypothetical reaction above if the products concentrations [Z] and [Y] are (a) separated quickly soon after they form (e.g. by gravity, magnetic, electrical or distillation type processes that can separate reactants from each other) or (b) the products are made cooler than reactants, by providing heated reactants, or if (c) the catalyst employed enables only the forward reaction; then the forward reaction is compelled to continuously happen even when the Ea for the backward reaction could be somewhat lower than for the forward reaction.  An open process can achieve a steady state conversion while maintaining very high productivity.  Thus the use of higher temperature reactant(s) can again be the best way to increase productivity. What are the main factors for best technical productivity? Examples from metals /chemicals industry.  What are the options for increasing temperature?  What are the best options for instant on-demand superheated steam at variable temperatures?