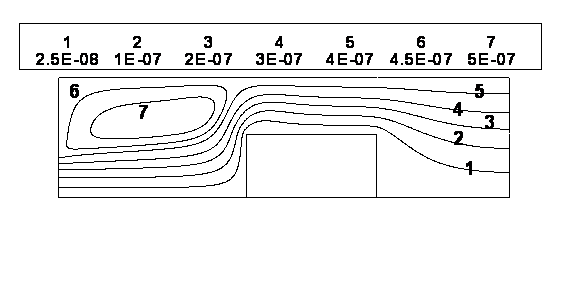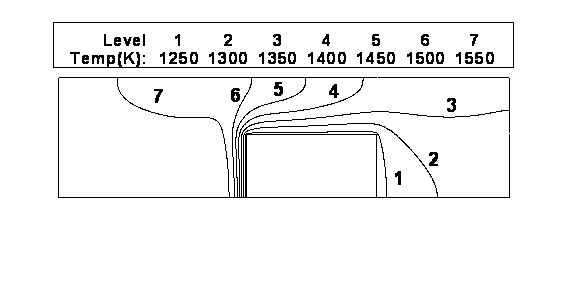Heat
Transfer Enhancement using Weakly-Ionized, |
Experimental measurements and
computational analysis of heat transfer in atmospheric pressure, mid-temperature
range (1200K-1600K) plasma flow over an aluminum cylinder have been
carried out. A comparison of
transient temperature measurements for the aluminum cylinder under
convective unionized air flow and those with convective plasma flow
shows significantly higher heat transfer from plasma flow compared
to air flow under identical temperature and flow conditions.
A heat transfer problem is computationally modeled by using
available experimental measurements of temperature rise in the cylinder
to determine the degree of ionization in the plasma flow. The continuity,
momentum, and energy conservation equations as well as conservation
equations for electrons and ions, and the Poisson’s equation for self-consistent
electric field are solved in the plasma by a finite volume method.
The conjugated transient heat transfer in the cylinder and in the
plasma is obtained by simultaneous solution of the transient energy
conservation equations. It is shown that the enhancement of heat transfer
in plasma flow is due to the energy deposited by charged species during
recombination reaction at the solid surface. An important finding
is that even a small degree of ionization (< 1%) provides significant
enhancement in heat transfer. This enhancement in heat transfer can
lead to productivity increase in metallurgical applications. Table of Symbols
Symbol Description
Units D
Diffusivity
m2/s e
Electron
charge
C h Heat transfer
coefficient
w/m2K k Boltzmann
Constant
J/K m
Mass
kg N
Number
Density
1/m3 p
Pressure
Pa Pr Prandtl
Number
q
Heat Transfer
Rate
W
r
Radial
coordinate
m R
Radius
m Re Reynolds
Number
Sc Schmidt Number
T Temperature
K t
Time
s u
velocity
m/s V
Voltage
V x
Axial
coordinate
m Greek Letters a Thermal diffusivity m2/s
Subscripts i Ion e electron w, s wall
Introduction Flow of
plasma, or ionized gas, is used in a variety of materials processing
and metallurgical applications including plasma spray coating, arc
welding, near net-shape manufacturing, plasma vapor deposition, polymer
deposition, and wire bonding in microelectronic chips [1, 2]. Based
on the temperature and pressure range, the plasmas used in these applications
can be divided in two primary types. First are the systems that use
high temperature and atmospheric or near-atmospheric pressure ionized
gas, also referred to as thermal plasmas. The condition of Local Thermodynamic
Equilibrium (LTE) is reached in thermal Plasma with temperatures around
10000 K and electron densities ranging from 1021 to 1026
m-3. The high temperatures prevalent in thermal plasmas
are useful for heating and melting of ceramic and metallic particles
in coating and welding applications and in destruction of bio-hazardous
materials. The second type of systems use the low pressure, low temperature
plasmas. The operating pressure and gas density are very low. There
is a significant difference in electron and heavy particles (neutral
and ions) temperature due to weak collision coupling between them.
The temperature of ions and neutral molecules is typically close to
room temperature. The abundance of ionized species in this type of
plasma is used to aid in chemical reactions in vapor deposition and
polymer processing. Heat transfer
in plasma flow has received much attention in the literature, in the
1960s and 1970s mainly in the context of electrostatic probes and
in aerospace applications, whereas in the last thirty years mainly
in the context of plasma-aided manufacturing. Available reviews [3,
2] provide detail discussion of a number of factors that affect the
heat transfer to a solid body from plasma. It is noted that the analysis
of heat transfer from plasma to a solid surface is significantly more
complicated as compared to unionized gas flow because it not only
involves the hydrodynamic and thermal boundary layers encountered
in unionized gas flows, but also electrical effects due to the presence
of charged species. These electrical effects arise due to the difference
in mobilities of ion and electron. The electrons having very high
mobility travel faster towards the surface and give rise to a negative
potential at the solid surface [4]. This negative potential repels
electrons and attracts ions. Subsequently the flow of ions and electrons
towards the surface becomes equal and the surface potential remains
constant thereafter. The surface potential when both the ion and electron
fluxes become equal is called the floating potential [4]. These charged
species recombine at the surface and release energy equivalent to
their ionization potential to the surface. Therefore the electric
field and charged species transport play an important role in determining
the heat transport to the surface [2, 3, 5, 6].
Atmospheric
pressure, high temperature thermal Plasmas have been studied extensively. Review [7] and a monograph [3] provide detailed
discussion of the work published in literature. Heat and momentum transfer to spherical particles
in thermal plasma has been studied extensively for the application
of plasma spray coating [7 and references therein]. A unified treatment
of heat transfer under continuum and non-continuum conditions has
been developed [8]. Correlations for Nusselt number have been proposed
for thermal plasma flow over spherical particles [9].
These correlations have been employed by several researchers
in computational analysis of plasma spray systems (see for example,
Proulx et al., [10]). However
these correlations ignore the electrical effects. For plasmas at low
pressure, heat transfer to a solid has been investigated applying
results from kinetic theory of rarefied gases [11, 12].
Unfortunately,
these two extremes (very hot plasmas at atmospheric pressure or cold
plasmas at low pressures) are not best suited for common metallurgical
work. For example, most of the aluminum melting or steel heat treatment
is carried out between 900 K and 1500 K. The low pressure plasma possesses
very low energy density and can not be used for aluminum melting.
The very high temperature thermal plasmas result in significant heat
losses and may result in poor efficiencies. Only recently, atmospheric pressure convective
plasma torches have become available that provide mid-temperature
range plasma (1200 K – 1600 K) at atmospheric pressure. These plasma
torches are being considered for aluminum melting, continuous flow
plasma chemical reactors, surface heat treatment and remediation of
biohazards and toxic wastes. However,
plasma flows under these conditions are not yet well characterized. To design and improve mid-temperature plasma
devices, the ability to predict the plasma flow over a solid body
and the concomitant heat transfer, is highly desirable.
In this
paper, we report experimental measurements of temperature rise in
an aluminum cylinder exposed to air flow and plasma flow under identical
temperature and flow conditions. The
results show significant increase in heat transfer with plasma flow.
Computational modeling for air flow and plasma flow have been carried
out to determine the degree of ionization in the plasma and to analyze
the heat transfer phenomena in the two cases.
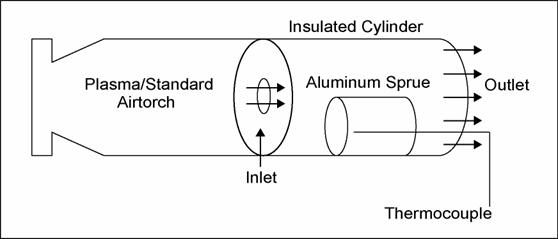
Experimental Setup: A
schematic of the experimental setup is shown in Figure 1. The setup consists of an insulated cylindrical
chamber. An Airtorch
[a]
or a Plasmatorcha is connected to the
chamber on the left and the high temperature gas enters the chamber
through the opening along the centerline of the chamber.
A thermocouple is placed at the entrance of the chamber to
measure the temperature at the exit of the torch.
An aluminum sprue is placed in the chamber with a thermocouple
attached to the sprue through a hole drilled from the back of the
sprue along its centerline. The thermocouple is at a location, 12mm
from the front surface, along the centerline. The K type thermocouple
was used which can record temperatures up to 1500 K. The air torch
exit temperature was measured with a B type thermocouple.
Both thermocouples were connected to a data acquisition system
for transient temperature measurements. An MHI DACs data acquisition
system was employed for the thermal measurements and the sampling
rate was 1 Hz. The mass flow rate was measured at the inlet and the
average velocity at the inlet of the insulated chamber was calculated
based on the measured temperature. Temperature
measurements were carried out with two identical aluminum sprues of
38.7mm diameter and 39mm length. In
the first case, an air torch was used to provide the gas at 1573 K
for convectively heating the sprue.
Transient temperature measurements were recorded.
In the second case, a plasma torch was used.
In this case, a weakly ionized gas from the torch provided
the convective heating of the sprue.
Once again, transient temperature change was measured for the
sprue interior. The sprue heated with the plasma torch resulted
in substantially higher heating rate compared to one heated with the
air torch. The experimental
measurements are discussed later in detail with the computational
predictions. Computational Analysis A flow
of weakly ionized gas consisting of neutrals, ions and electrons over
a cylindrical aluminum sprue is considered. The far field pressure
is atmospheric and the flow Reynolds number based on the inlet velocity
and sprue diameter is in the laminar range. As
the degree of ionization is expected to be small, the overall velocity
field can be found from the solution of the continuity, momentum,
and energy equations for the neutral gas flow field [13]. The flow
was considered to be steady and axisymmetric, however the temperature
field was considered transient due to heating of the sprue. Gas thermophysical
properties were evaluated at the far field temperature. The neutral
gas flow in the chamber and conduction in the sprue were computationally
modeled by using FLUENT 6.2.1 commercial flow/thermal solver. Using
GAMBIT 2.1, a 2-D axisymmetric mesh was generated using the dimensions
given in the experimental setup. The mesh generated was highly refined
in order to facilitate greater accuracy in the numerical solution
and to account for steep gradients near the sprue. Using
the velocity field, a computational model was developed to evaluate
the electron and ion flux and the self-consistent electric field.
A separate program was developed to determine
the number density of charged species and the electric field as described
below. The charged species flux to the surface was then evaluated
and the contribution to heat transfer due to recombination of electron
and ions was determined. Using
the following dimensionless quantities:
The governing equations in dimensionless
form are: Mass conservation
Momentum conservation
Energy conservation in the plasma
Energy conservation in the sprue
Neglecting production and recombination
of the charged species in the bulk of the flow, the conservation equations
for the charged species number densities and the governing equation
of the self-consistent electric field can be written as follows. Continuity Equations for electrons
Continuity Equations for ions
Poisson equation for electric
field
The ion and electron fluxes are
given by
The plasma and air are considered
optically thin and the radiation transport is considered between sprue
surface and the container wall. Since the gas is at atmospheric pressure,
the difference in temperature between the neutral gas and the charged
species was assumed to be small throughout the flow domain (
The flow field for the computational
domain is obtained first by solving equations (1) and (2) in FLUENT
flow/thermal solver. The SIMPLE algorithm for pressure correction
was employed and discretization was carried out using the Power-law
method as described in Patankar [14]. An under relaxation technique
was used for the momentum equation. The solution of these equations
provides the flow field in the entire domain. The equations (3) - (7) are solved to obtain
the number density distribution of the ions and electrons and the
electric potential in the plasma as well as temperature distributions
in the plasma and the sprue. A finite difference method was employed
to discretize equations (3) – (7) based on the Alternate Direction
Implicit Scheme [14]. A computer program was developed to iteratively
solve the resulting tri-diagonal systems of equations using the Thomas
algorithm. We expect to have steep gradients in velocity and temperature
near the sprue surface. To resolve these steep variations a very fine
grid was taken. The convergence criterion was set at 1x 10-6
of relative error between successive iterations at all points.
Thermophysical properties for charged species were obtained from Refs.
[15] and [3]. For the case of heating from unionized air flow, the
methodology is similar to the one described above, however equations
(5) – (7) are not needed. Boundary
Conditions The governing equations were solved
with the following boundary conditions. The sprue surface was considered
as a perfect sink for the charged species
Results and Discussion In a computational
study, it is important to evaluate the effect of grid spacing on the
solutions to make sure that the results are grid-independent. The
computations were carried with different grid sizes until the solution
was insensitive to the grid size. The node points were doubled until
the computed heat transfer coefficient at the sprue surface changed
by less than 0.1%. The final grid had 721 points in the axial direction
and 193 points in the radial direction. Heat
transfer in air flow Using
this grid, we first considered the flow from an air torch in the analysis. The streamlines for the flow are shown in Figure
2. It is clear from the figure
that as the flow goes around the sprue, a re-circulating flow pattern
is obtained. Due to the decrease
in the cross-sectional area due to the presence of the sprue, the
velocity increases as the gas moves along the container walls. The temperature
contours obtained for the flow domain are shown in Figure 3. Most of the region in the upstream of the sprue
the temperature is nearly uniform. Due to the re-circulating vortex
patterns on the downstream region from the sprue, colder fluid from
the sprue mixes with the hotter fluid away from the sprue. This is
evident from the temperature contours. The temperature contours show
that the heat transfer rate is maximum at the front surface of the
sprue and as there is a sharp change in gas temperature near the surface.
As the flow proceeds toward the outlet there is a decrease in the
heat transfer rate on the top surface of the sprue. This is evident
from the temperature contours showing temperature drop over a larger
distance compared to the front surface. The heat transfer coefficient
was obtained at all points along the surface of the sprue by equating
the net heat transfer to the surface from gas flow to the product
of heat transfer coefficient and the temperature difference between
the inlet temperature and the surface temperature as
Heat
Transfer in Plasma Flow With plasma
flow, number densities of charged species and the induced electric
field are determined. Figure
4 (a) and (b) show the dimensionless ion and electron density contours,
respectively with degree of ionization at the inlet as 0.64%. The motion of the charged species is the net
effect of convection, diffusion, and drift under the influence of
electric field. Both ion and electron are convected with the same
neutral flow. However, electric field has opposite effect on the motion
of ions as compared to that of electrons.
As the electric potential at the surface is negative, it results
in repelling electrons and attracting ions. Not surprisingly, the
number densities of electrons are low closer to the surface whereas
ion densities are higher near the sprue surface. The recombination reaction of charged species
at the surface gives energy equal to the ionization potential to the
surface. Figure
5 shows the transient temperature measurement with the thermocouple
placed in the sprue interior. The
significant increase in the rate of temperature rise indicates higher
heat transfer with plasma heating as compared to heating with air
flow. To validate our model, we first compared the
computational results of temperature rise with the experimental measurements.
As seen in the figure, the computational results match well
with experimental measurements. Next, to determine the degree of ionization
in plasma, a parametric study was conducted by considering different
values of inlet ion and electron number densities. The predicted values
of the temperature rise with different degree of gas ionization were
compared with the experimental measurements of temperature change
in the sprue interior with plasma heating.
This gave the degree of ionization as 0.64% for the case considered
here. The predicted results for 0.64% ionization are shown in Figure
5. The influence
of ionization on heat transfer enhancement is plotted in Figure 6.
The figure shows the area weighted average heat transfer coefficient
as a function of the degree of ionization at the inlet. With increase
in the degree of ionization the number densities of charged species
and hence the flux of charged species to the sprue surface increases.
This leads to higher heat transfer to the sprue surface and
the enhancement of heat transfer is seen to increase nearly linearly
with degree of ionization. For the first case with no ionization,
the average heat transfer coefficient was 28.2 W/m2K, whereas
with plasma flow with 0.64% ionization the heat transfer coefficient
was 39.2 W/m2K. A change in the gas ionization from 0 to 0.64%
resulted in approximately 40% increase in the average heat transfer
coefficient. It may be noted that the model presented here is restricted
to weakly ionized gas and as such the results should not be directly
extrapolated beyond 1% ionization unless field effects are incorporated.
Summary
and Conclusions Transient
temperature measurements and computational simulation of convective
heating of an aluminum sprue was carried out.
Two cases were considered, one with heating by unionized air
flow and the other with plasma flow.
Transient temperature rise in the sprue interior was measured
and it showed significant increase in heat transfer with plasma flow
compared to air flow under identical temperature and flow conditions.
To computationally simulate the process, the flow of continuum, axisymmetric,
laminar, mid-temperature range (1200K – 1600K) plasma flow over a
cylinder was modeled using a finite volume method. The continuity and the momentum conservation
equations for the flow were solved using commercially available FLUENT
flow/thermal solver. Using the flow field, a computational model was
developed to solve the governing equations for the conservation of
electrons and ions and the self-consistent electric field as well
as the energy conservation in the gas flow and the sprue interior.
The governing equations were discretized using a finite volume method
and the resulting system of equations was solved by Alternating Direction
Implicit scheme. Transient heat transfer to the cylinder was evaluated
by considering convective heat transfer from the neutral flow, the
energy transport by radiation between the sprue surface and the wall,
and the energy deposited by recombination of charged species at the
cylinder surface. Results for transient temperature rise in the
cylinder with air heating were used to validate the computational
model. The degree of ionization present in the plasma flow was determined.
The following conclusions can be drawn from this part of the study.
References:
Figure Captions Figure
1.
A schematic of the experimental setup Figure
2.
Flow stream lines Figure
3.
Temperature contours with air torch heating (K). Figure
4.
(a) Dimensionless ion number density contours and (b) Dimensionless
electron number density contours Figure
5.
Comparison of computational predictions and experimental measurements
of temperature increase in the sprue Figure
6.
Variation of heat transfer coefficient with the degree of ionization
Figure
1.
A schematic of the experimental setup
Figure 2. Flow stream lines
Figure 3. Temperature contours
with air torch heating (K).
(a)
(b) Figure
4.
(a) Dimensionless ion number density contours and (b) Dimensionless
electron number density contours
Figure
5.
Comparison of computational predictions and experimental measurements
of temperature increase in the sprue.
Figure
6.
Variation of heat transfer coefficient with the degree of ionization |